字串失敗機率分析

失敗機率會小於等於 n / P

當 Hash 碰撞發生時，會將不同的字串判斷成相同，機率上限為 n / P。

把字串當成一個多項式 $a_0{x}^0+a_1{x}^1+a_2{x}^2+\dots a_{n-1}{x}^{n-1}(\mathrm{mod}P)$$a_0 x^0 + a_1 x^1 + a_2 x^2 + \dots a_{n-1} x^{n-1} \pmod{P}$

兩個長度 n 的字串 a, b 相等表示兩個多項式 a - b = 0。多項式 a - b 最多會有 n 個根¹ ⇒ 失敗機率會小於等於 n / P

更詳細可見 : https://codeforces.com/blog/entry/60442

字串題目分析一般當成 1 / P

上面分析說 n / P 其實是高估很多的，因為還需要多項式恰好有 n 個根。在一般的情況下，會將不同的字串判斷成相同的機率是 1 / P。

令 $P_s(x),P_t(x)$$P_s(x),P_t(x)$ 是 $s,t$$s,t$ 多項式帶入 $x$$x$ 的 hash value。我們假設 $P$$P$ 很大，使 $P_s(x),P_t(x)$$P_s(x),P_t(x)$ 以 $x\in \mathbb{Z}$$x \in \mathbb{Z}$ 代入都是介於 $[0,P-1]$$[0,P-1]$ 的 uniform random number²。

若 $s=t$$s=t$ :

• $\mathrm{\forall }x\in \mathbb{Z}{P}_s(x)=P_t(x)$$\forall x\in \mathbb{Z}\space \space P_s(x)=P_t(x)$

若 $s\ne t$$s\neq t$ :

• $\frac{P-1}{P}$$\frac{P-1}{P}$ 大多數 $P_s(x)\ne P_t(x),x\in \mathbb{Z}$$P_s(x)\neq P_t(x),x\in \mathbb{Z}$

• $\frac{1}{P}$$\frac{1}{P}$ 少數 $P_s(x)=P_t(x),x\in \mathbb{Z}$$P_s(x)= P_t(x),x\in \mathbb{Z}$

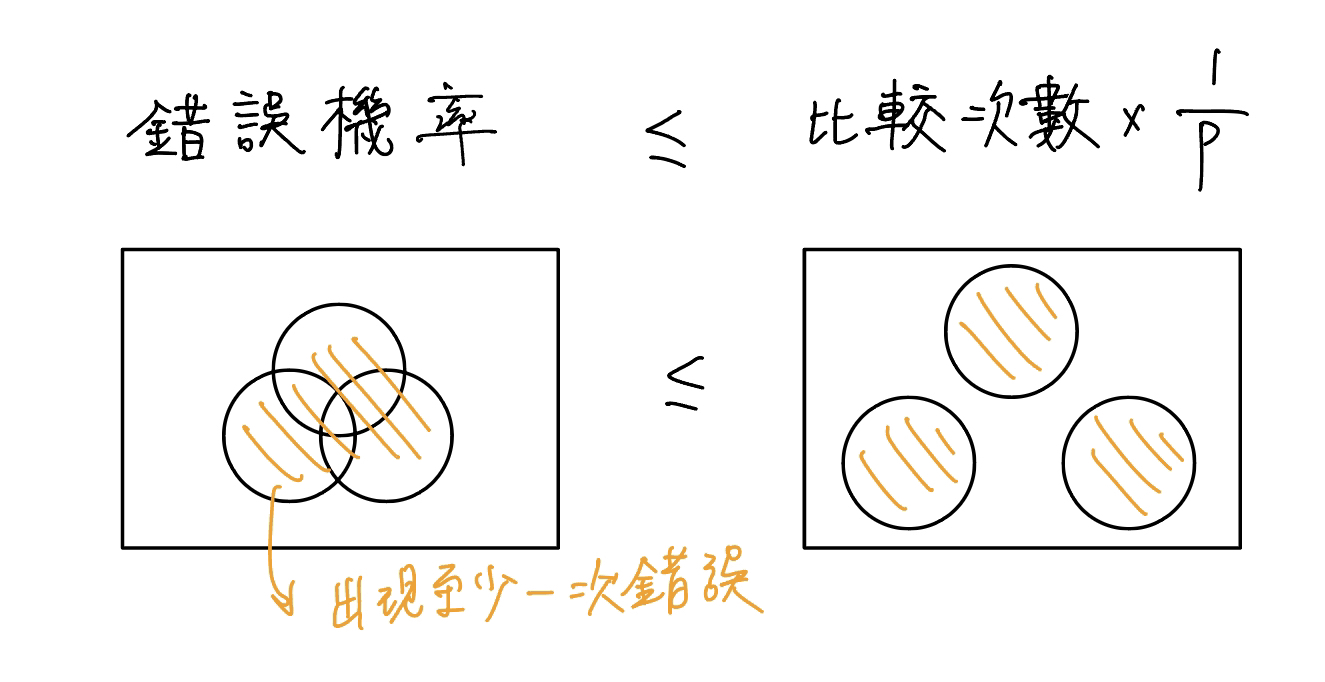
n 次比較錯誤機率 <= n / P

每次比較兩個字串 s, t 是否相同，進行 n 次，會至少出現一次錯誤的機率 <= n / P。

例如我們比較 3 次，一次的失敗機率為 1 / P。我們將圖畫出來 :